Expressing relationship between two-numbers as a percentage based on their quotient
Or, numbers are fun and here is a way to wow someone
I love finding relationships in number-sets. A favorite memory from high school deals with a game we would play in Algebra class. The teacher would give us a set of numbers and one target number. The goal was to use the set of numbers and arithmetic operations to get to the target. Here is an example:
Set: \({1, 2, 4, 6}\)
Target: \(49\)
A couple solutions: \([1 + (2 * 4) * 6], [1 + 2 * (4 * 6)]\)
You can find problems like this in a handy desk calendar (non-affiliate link).
Fast forward several years and I started thinking about age as a percentage between a parent and child. It seemed interesting that a child is half the age of their parent when the child is the same age as the parent when the child is born. At first, I thought this was a fluke of the number-world, but gave it more thought, given both child and parent age at the same numerical-rate. I was interested in finding a general-purpose equation–one that could be applied at any age and came up with: \(a = (b + a)c\), where \(a\) is the child's age, \(b\) is the age of the parent when the child is born, and \(c\) is the relationship between both as a percentage. Let us go through an example:
My Dad is thirty years old when I am born. When I am ten, what percentage of my Dad's age am I?
Solution:
\(10 = (30 + 10)c\)
\(10 = 40c\)
Divide both sides by 40
\(c = 10 / 40\)
\(c = 0.25\) or 25%
What I really want to do, though, is find age based on percentage. Now, the question becomes what is my age when I am twenty-five percent of my Dad's age? Taking the original equation, we can work to get \(a\) on one-side:
\(a = (b + a)c\)
Distribute the right-side
\(a = bc + ac\)
Subtract \(ac\) from both-sides
\(a - ac = bc\)
Factor \(a\) from the left-side
\(a(1 - c) = bc\)
Divide both sides by \((1 - c)\)
\(a = (bc) / (1 - c)\)
And plugging our numbers into the equation:
\(a = (30 * 0.25 ) / (1 - 0.25)\)
\(a = 7.5 / 0.75\)
\(a = 10\)
But, we can do even better–we can also answer the question what is the age of my Dad when I am twenty-five percent of his age? Again, looking at the original equation, we can create a new variable \(d\) and put it in place of \((b + a)\):
\(a = dc\)
Divide both sides by \(c\)
\(d = a / c\)
We already solved for \(a\), so we can put it into the equation:
\(d = ((cb) / (1 - c))/c\)
Let us convert the outer division problem into multiplication for better readability
\(d = ((cb) / (1 - c))(1 / c)\)
Multiply both numerators and denominators
\(d = (cb) / (c - c^2)\)
Factor \(c\) from the denominator
\(d = (cb) / (c(1 - c))\)
We can now remove \(c\) from both numerator and denominator
\(d = b / (1 - c)\)
And plugging our numbers into this equation:
\(d = 30 / (1 - 0.25)\)
\(d = 30 / 0.75\)
\(d = 40\)
Of course, these equations are not limited to comparing age. They can be applied to any two-numbers. The key is to represent \(b\) relative to zero. So, if \(a\) is not zero, then \(b\) becomes \(b-a\). Keep in mind, however, \(c\) cannot be one-hundred percent. This leads to division by zero. Lastly, for some extra visual flaire, we can graph the results using \(x = 30 / (1 - y)\). Keeping with our theme, this plots my Dad's age on the x-axis with my percentage (in decimal-form) of his age on the y-axis. Notice the asymptotic-nature of the line:

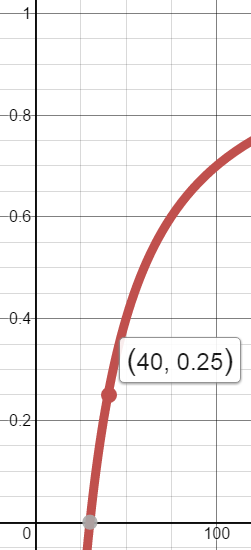
Graphs plotted using https://www.desmos.com/calculator.