Calculate height of objects

Knowing whether a tree has the potential to crash into your house

March 31, 2016

Here is a classic scenario: Local would-be lumberjack decides to cut-down tall tree right beside house. Tree falls towards house. Disaster ensues. Others have a laugh at the homeowner's expense. This post will not help if you find yourself in a similar situation. Instead, this post will allow you to make an informed decision when that tree has a little bit of distance between itself and the house and its height makes the outcome a little blurry.

Tools you will need

Calculator with \(tan\) function.
Measuring tape or another reliable method to measure distance.
Clinometer or protractor, tape, drinking straw (no bendy straws), string, and quarter (or another small and similar-weighty object).
- Alternative is an app. for your phone (i.e. https://play.google.com/store/apps/details?id=com.plaincode.clinometer).

Build a homebrew clinometer

If you are you going the phone-app. route or already have a clinometer, skip this part.

Put the protractor on a table.
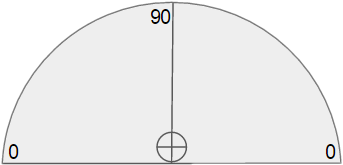
Flip the protractor upside-down.
Tape the straw near the flat-edge of the protractor.
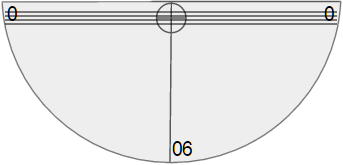
Cut a piece of string so its length is greater than the height of the protractor.
Tape one end of the string to the quarter.
Tape the other end of the string to the center of the protractor right below the straw.
- Make sure the direction of the string is oriented so the quarter goes below the curve of the protractor.

How to use the homebrew clinometer

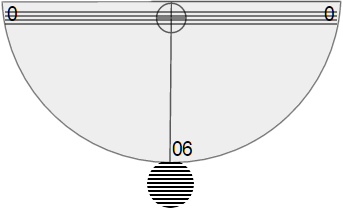
Look through the straw and up to the top of an object.
The string/coin combination will have moved to a new spot on the protractor.
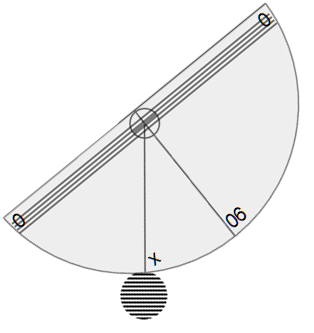
Read the number below the string and subtract from ninety.
- Depending on the particular protractor, this number may be greater than ninety. If so, just take the absolute-value of the result.
- It may be easier to have someone else tell you the number.
The result tells us the angle of inclination.

Finding the height of the tree

In order to do this effectively, the area surrounding the tree needs to be flat-ground. Any slope will produce inaccurate results.

Measure the distance between the house and tree. This becomes our baseline and determines whether the height of the tree will cause it to potentially hit the house.
Back away from the tree in any direction until you get a comfortable view of the tree-top. You will need to measure your distance from the tree.
Take a reading from the clinometer.

Tangent to the rescue

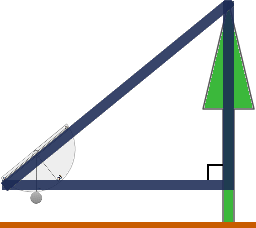
Tangent is a trigonometric function leveraging two-sides of a right triangle and is defined as: \(tan\theta = "opposite"/"adjacent"\). In our case, we know \(\theta\) (our clinometer reading) and the \("adjacent"\)-value (distance from inclination measurement to tree). To get \("opposite"\) (height), we just re-order the equation: \("opposite" = tan\theta * adjacent\).

Example

Distance to tree: \(20 ft.\)
Inclination: \(50°\)
height = \((tan50) * 20\)
height = \(~24 ft.\)

But wait, there's more...

Unless the clinometer reading took place on the ground, we need to add the height the reading occurred to our previous result. This is normally the distance from your eyes to the ground. For our example, we will go with fifty inches. Then, our estimated height becomes: \(24 ft. + 50 "in." = 28 ft. 2 "in."\). Lastly, take the estimated value and subtract from the previously obtained baseline.

If the result is negative, the tree will hit the house if it falls towards the house.
If the result is close to zero, then you must like to gamble.
If the result is positive, then you are pretty safe from direct contact. Of course, I would still want a pretty big buffer like ten feet or so (and more for a taller tree).

45°–45°–90° rule

If you want to bypass using \(tan\), then use this shortcut. Given the sum of all interior angles of a triangle equal 180 and we already know one-angle of our imaginary triangle is ninety, then if our clinometer-angle is fourty-five, the remaining angle is also fourty-five. With these angles, the two sides of importance to us are equal. This means the only measurement needed is from the clinometer reading-point to the tree!

Conclusions

While both methods for calculating height are effective, they both depend on a couple factors:

Accuracy of distance measurements.
Accuracy of clinometer reading.

The clinometer will most-likely be the greatest source of error. The further the reading moves away from fourty-five degrees, the greater the potential for error (\(tan45 = 1\)). If you are getting readings in the eighties, either you are dealing with a super tree, or you are just too close to the tree. Lastly, be careful and take several measurements. And remember, if you decide to cut down the tree, sometimes it is better to hire a professional.